与えられた直線角の中に、与えられた直線図形に等しい平行四辺形を作ること。
命題42から、三角形に等しい平行四辺形の作図を見てきた。今回はこれまでの集大成として、直線図形に等しい平行四辺形を作図したい。
「集大成」と言ったのはあながち大袈裟ではなく、今回の証明にはこれまでに登場した命題が大集合する。特撮かアニメの最終回のようだ。
直線図形ΑΒΓΔと、角Εが与えられたとする。このとき、与えられた角Εの中に、直線図形ΑΒΓΔに等しい平行四辺形を作りたい。
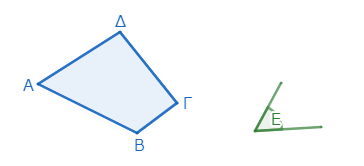
ここでは直線図形として四角形を描いているが、この命題の方法は四角形でなくても成り立つ。このことについては、またあとで触れよう。
では作図していこう。まず、ΔΒを結ぶ*1。そして、三角形ΑΒΔに等しい平行四辺形ΖΘを、角Εに等しい角ΖΚΘの中に作る*2。

そして、線分ΗΘ上に、三角形ΔΒΓに等しい平行四辺形ΗΜを、角Εに等しい角ΗΘΜの中に作る*3。
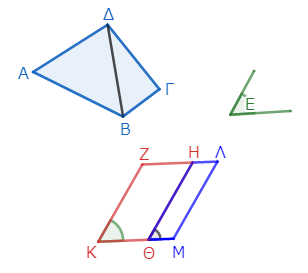
このとき、描かれた図形ΖΚΘΜΛΗが、求める平行四辺形である。要は、直線図形を三角形に分割し、それぞれの三角形に等しい平行四辺形を繋げて描いてやればよい。
では、これで作図できていることを証明しよう。主題は、図形ΖΚΘΜΛΗが平行四辺形だと証明することだ。そのために、ΚΘΜとΖΗΛが直線であること、そして互いに等しくかつ平行であることを示そう。
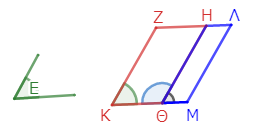
まず、角Εが角ΖΚΘ、角ΗΘΜの双方に等しいので、角ΖΚΘは角ΗΘΜに等しい*4。双方に角ΚΘΗを加えれば、角ΖΚΘと角ΚΘΗの和は、角ΗΘΜと角ΚΘΗの和に等しい*5。そして角ΖΚΘと角ΚΘΗの和は二直角に等しい(なぜなら二線分ΚΖ、ΘΗは平行線であり、平行線の同側内角の和は二直角に等しいので)*6。よって角ΗΘΜと角ΚΘΗの和も二直角に等しい*7。ゆえに線分ΚΘは線分ΘΜと一直線を成す*8。

線分ΚΘΜと線分ΖΗは平行であり、そこに線分ΗΘが交わっているので、錯角ΜΘΗ、ΘΗΖは等しい*9。双方に角ΘΗΛを加えると、角ΜΘΗと角ΘΗΛの和は、角ΘΗΖと角ΘΗΛの和に等しい*10。二線分ΘΜ、ΗΛは平行線なので、同側内角ΜΘΗ、ΘΗΛの和は二直角に等しい*11。ゆえに角ΘΗΖと角ΘΗΛの和も二直角に等しい*12。ゆえに二線分ΖΗとΗΛは一直線を成す*13。
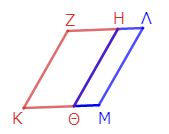
さて、二線分ΖΚとΗΘは平行四辺形ΖΘの対辺なので、等しくかつ平行である*14。同様に二線分ΗΘとΛΜも平行四辺形ΗΜの対辺なので、等しくかつ平行である*15。ともにΗΘに等しくかつ平行なので、ΖΚとΛΜも互いに等しくかつ平行である*16*17。等しくかつ平行な二線分を、二線分ΚΜ、ΖΛが同じ側で結んでいるので、ΚΜとΖΛもまた等しくかつ平行である*18。ゆえに図形ΖΚΘΜΛΗは、対辺が平行な四辺形なので、平行四辺形である。
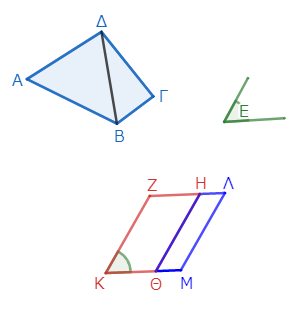
そして三角形ΑΒΔは平行四辺形ΖΘに、ΔΒΓはΗΜに等しいから、直線図形ΑΒΓΔ全体は平行四辺形ΖΚΜΛ全体に等しい*19。
よって与えられた直線図形ΑΒΓΔに等しい平行四辺形ΖΚΜΛが与えられた角Εに等しい角ΖΚΜの中に作られた。これが作図すべきものであった。
長い。もっと簡潔な証明はなかったのだろうか。たとえば四角形の内角の和が四直角に等しいことがわかっていれば、もう少し簡略化できただろう。しかしここまでの命題にそんな定理は存在しない。結局、この長い証明しかないのだろう。
冒頭で、今回の証明は集大成だなどと大見得を切ったが、それは命題14「二直角は直線」や命題30「三線分の平行」が初めて他の命題に登場したからだ。私は初めてこの命題を読んだとき、「お前こんなところに出てくるのかよ」と感嘆した。こんな後半の命題のために伏線を張っていたのかと思うと感慨深い。
上記では直線図形として四角形を採用しているが、作図の方法を見れば明らかなように、四角形に限らず多角形であれば同様に作図が可能だ。いかなる多角形も三角形に分割可能なので、それぞれの三角形に等しい平行四辺形を描いてやればよい*20。
証明という観点から考えれば、一般の多角形(n角形)に関して作図可能であることを示すべきである。現代人なら、「n角形をn-2個の三角形に分割する」と始めれば、一般の場合で証明できる。しかしユークリッドは、四角形(n=4)の場合しか示していない。
実は今回に限らず、同様に考えれば一般の場合にも成立するとき、ユークリッドは一般の場合の証明について触れないことがある。特に第7~9巻の「数論」でそれは顕著だ。
これは、やらなかったのではなく、できなかったのだと考えられている。なぜなら、ユークリッドの時代には文字式がなかったからだ。現代ならば自然数をnとおいて一般的な証明を行うが、ユークリッドにはそれができなかった。そこでユークリッドは、n = 2, 3, 4など特別な場合で証明を行い、一般の場合にも成立することを推測するに留まらざるを得なかった。
このような方法を、「準一般的」と呼ぶ。今回の命題も、準一般的な作図方法を示せたので、一般のn角形についても同様に成り立つだろうと推測したのだ。
そういえばこれまでの命題の中で、複数通りに作図できるにも関わらず、一通りの作図しか行わないことがあった(例えば命題24)。どうしてそんな中途半端な証明をしているのかずっと疑問だったが、もしかしたらこのような時代背景が原因の一つなのかもしれない。つまり、特別な場合で証明できれば、一般の場合でも成り立つと考えるのが普通だったのかもしれない。
今回、さらりと二段落で作図が完了してしまっているが、実際にこの作図を行うのはかなり面倒だ。以下が、今回の作図の全容である。
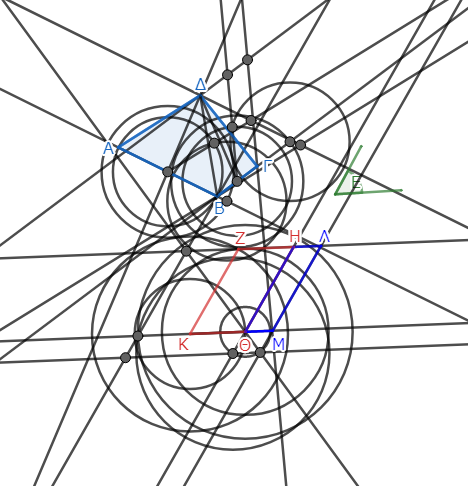
見ただけでとんでもない作図だと分かるかと思う。しかも、これでも線は少ない方なのだ。
当ブログの作図は主にGeoGebraというフリーソフトで行ってる。GeoGebraは「指定した二点を通る直線を引く」「中心と円周上の一点を指定して円を描く」など、定木とコンパスを模した機能を使って作図できるソフトだ。しかしこれだけで図を描くのは大変なので、「指定した半径で任意の場所に円を描く」「指定された点を通る平行線を描く」などの機能もある。これらを駆使して描いたものが上図なので、本気で作図しようと思うとさらに線が増える。
これまでにも何度か、「ユークリッドは理論上描けるかどうかだけを重視して、実際上描けるかどうかはあまり気にしていない」と主張してきたが、今回の命題もその証拠のひとつになるだろう。
(2018/02/21追記)今回の「与えられた直線上に、与えられた図形に等しい平行四辺形を作図する問題、およびその解法」を領域付置と呼ぶ。命題41「平行四辺形は三角形の二倍」からここまで、我々は領域付置のために命題を証明してきたのだ。
領域付置は、今後も『原論』の中でたびたび登場する、重要な技法である。
*2:命題42「与えられた直線角の中に与えられた三角形に等しい平行四辺形を作ること」
*3:命題44「与えられた線分上に与えられた三角形に等しい平行四辺形を、与えられた直線角に等しい角の中に作ること」
*4:公理1「同じものに等しいものはまた互いに等しい」
*5:公理2「等しいものに等しいものが加えられれば、全体は等しい」
*6:命題29「一つの直線が二つの平行線に交わって成す錯角は互いに等しく、外角は内対角に等しく、同側内角の和は二直角に等しい」
*7:公理1「同じものに等しいものはまた互いに等しい」
*8:命題14「もし任意の直線に対して、その上の点において同じ側にない二直線が接角の和を二直角に等しくするならば、この二直線は互いに一直線を成すであろう」
*9:命題29「一つの直線が二つの平行線に交わって成す錯角は互いに等しく、外角は内対角に等しく、同側内角の和は二直角に等しい」
*10:公理2「等しいものに等しいものが加えられれば、全体は等しい」
*11:命題29「一つの直線が二つの平行線に交わって成す錯角は互いに等しく、外角は内対角に等しく、同側内角の和は二直角に等しい」
*12:公理1「同じものに等しいものはまた互いに等しい」
*13:命題14「もし任意の直線に対して、その上の点において同じ側にない二直線が接角の和を二直角に等しくするならば、この二直線は互いに一直線を成すであろう」
*14:命題34「平行四辺形において、対辺および対角は互いに等しく、対角線はこれを二等分する」
*15:命題34「平行四辺形において、対辺および対角は互いに等しく、対角線はこれを二等分する」
*16:公理1「同じものに等しいものはまた互いに等しい」
*17:命題30「同一の直線に平行な二直線はまた互いに平行である」
*18:命題33「等しくかつ平行な二線分を同じ側で結ぶ二線分は、それ自身等しくかつ平行である」
*19:公理2「等しいものに等しいものが加えられれば、全体は等しい」
*20:ただし、三角形に分割可能なことの証明はやや難しい。私も詳しく知らないので、知りたい方はググってほしい。なおユークリッドの時代にこの証明が知られていたかどうか、私は知らない。