第3巻命題26 等しい二円の円周角
等しい円において等しい角は、中心角も円周角も、等しい弧の上に立つ。
ひとつの円において、同じ切片内の角が互いに等しいことは既に示した。
ところがその逆、円周角が等しければそれらが上に立つ弧、あるいはそれを含む切片が等しくなることは、いまだ示していない。
にもかかわらず、それを二円に拡張した命題が、今回の命題3.26である。
早速証明しよう。
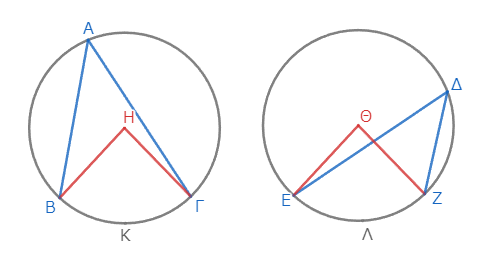
等しい二円ΑΒΓ、ΔΕΖがあり、それらの中心角ΒΗΓ、ΕΘΖが等しく、円周角ΒΑΓ、ΕΔΖも等しいとする。このとき、弧ΒΚΓと弧ΕΛΖも等しいことを示そう。
まず、ΒΓ、ΕΖをそれぞれ結ぶ*1。こうしてできる二つの三角形ΒΗΓ、ΕΘΖに注目しよう。
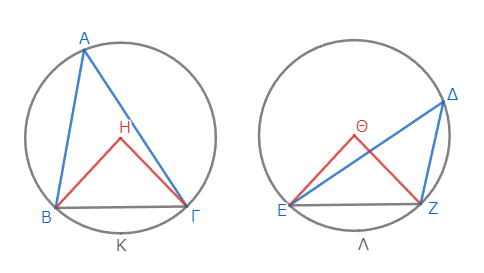
二円ΑΒΓ、ΔΕΖは等しいので、半径は等しい*2。したがって半径であるΒΗ、ΗΓは、同じく半径であるΕΘ、ΘΖに等しい。さらに、Ηにおける角はΘにおける角に等しいのだった。よって、これらの三角形は合同であり、底辺ΒΓは底辺ΕΖに等しい*3。
さて、Αにおける角がΔにおける角に等しいので、切片ΒΑΓは切片ΕΔΖに相似である*4。しかもこれらは、等しい弦ΒΓ、ΕΖの上にある。そして、等しい弦の上にある相似な切片は、互いに等しいのだった*5。ゆえに、切片ΒΑΓは切片ΕΔΖに等しい。
ところで、円ΑΒΓも円ΔΕΖに等しいので、ここから切片ΒΑΓ、ΕΔΖを除いた残りの弧ΒΚΓ、ΕΛΖもまた等しい*6。
よって、等しい円において等しい角は、中心角も円周角も、等しい弧の上に立つ。これが証明すべきことであった。
用語が『原論』特有のものである点を除けば、それほど難しい証明ではない。
三角形の合同から弦ΒΓ、ΕΖが等しいことを言い、弦が等しいことと切片内の角が等しいことから切片ΒΑΓ、ΕΔΖが等しいことを言う。等しい二円の中に等しい切片があるのだから、残りの弧も等しい、という論法だ。三段論法のようにすっきりしている。
ユークリッド的には、円から切片を除くと弧が残るらしい。『原論』では、円とは円板のイメージで書かれていることが多い。したがって円から切片を除けば、残るのは切片であるはずだ。しかし、ここではそうなっていない。
もしかしたら、「円」を円周の意味で使っているのかもしれない。あるいは、円と円周をあまり区別せずに使っているのかもしれない。
参考文献[4]のギリシャ語文を確認すると、証明の終盤の「円ΑΒΓも円ΔΕΖに等しいので」の部分は、次のようになっている。
ἔστι δὲ καὶ ὅλος ὁ ΑΒΓ κύκλος ὅλῳ τῷ ΔΕΖ κύκλῳ ἴσος·
ὅλος ὁ ΑΒΓ κύκλος が「円ΑΒΓ全体」を意味する。『原論』では、円は κύκλος 、円周は περιφερεία と書いているようなので、原文でも「円」と書いていることになる。
あるいは、「円の切片」の方のイメージが違うのかもしれない。第3巻の定義のページで、私は円の切片を下図のような塗りつぶしたものとして描いた。
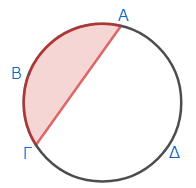
が、もしかしたら、こういう淵のイメージなのかもしれない。

もっとも仮にこうだとしても、円周からこれを除くと、弦の部分が「マイナス」になってしまう。
なのでユークリッド的には、上のイメージだろうが下のイメージだろうが、円周からこれを除けば弧しか残らない(ユークリッドには負の数のイメージがないはずなので)ということかもしれない。
円の切片の定義は、「弦と弧に囲まれた図形」であった。「囲まれた」と言っているので、やはり上の塗りつぶしたイメージが正しそうだ。
せっかくなので参考文献[4]でギリシャ語を確認しよう。こうなっている。
定義3.6
Τμῆμα κύκλου ἐστὶ τὸ περιεχόμενον σχῆμα ὑπό τε εὐθείας καὶ κύκλου περιφερείας.
最初の Τμῆμα κύκλου が「円の切片」、次の ἐστὶ が英語のbe動詞に相当する単語だ。
本題は次からだ。τὸ περιεχόμενον σχῆμα は「~にπεριεχόμενονされた図形」の意味である。何にπεριεχόμενονされたかというと、τε εὐθείας καὶ κύκλου περιφερείας である。これは「直線と円の弧」なので、「弦と弧」の意味だ。
で、問題は περιεχόμενον である。辞書を引くと、「to encompass(の現在分詞/受動態または中動態)」と出てくる。encompassとは「包囲する」「取り囲む」「包む」「覆う」などの意味の単語だ。
受動態で書かれているので、やはり弦と弧だけの淵の部分ではなく、その内側全体のことを指すと考えて間違いないだろう。
(ここまで書いて気付いたが、仮に淵を指すのなら、「弦と弧に囲まれた」ではなく「弦と弧を合わせた」といった書き方になるはずである)
私は冒頭で、
「円周角が等しければそれらが上に立つ弧、あるいはそれを含む切片が等しくなることは、いまだ示していない。にもかかわらず、それを二円に拡張した命題が、今回の命題3.26である」
と書いた。
だが参考文献[3]によると、この主張にはやや誤解があるらしい。参考文献[3]の解説にはこうある。
実際の適用場面では、2つの等しい円ではなく、同一の円の中で等しい二つの弧の上に立つ円周角に対してこの命題が適用される場合が多い(適用例としてIV.11 を参照)。
たしかに今回の証明は、等しい二円ではなく、同一の円の中でも成立する。こんな風な図を描けば良い。
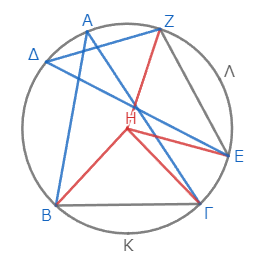
ゴチャゴチャした図になるが、今回の証明はこの図でも成立する(Ηを適宜Θに読み替える必要はある)。
参考文献[4]によると、今回の命題のギリシャ語文は以下の通りである。
命題3.26
᾿Εν τοῖς ἴσοις κύκλοις αἱ ἴσαι γωνίαι ἐπὶ ἴσων περιφερειῶν βεβήκασιν, ἐάν τε πρὸς τοῖς κέντροις ἐάν τε πρὸς ταῖς περιφερείαις ὦσι βεβηκυῖαι.
意味のまとまりごとに分けて訳すと、こんな風になる。
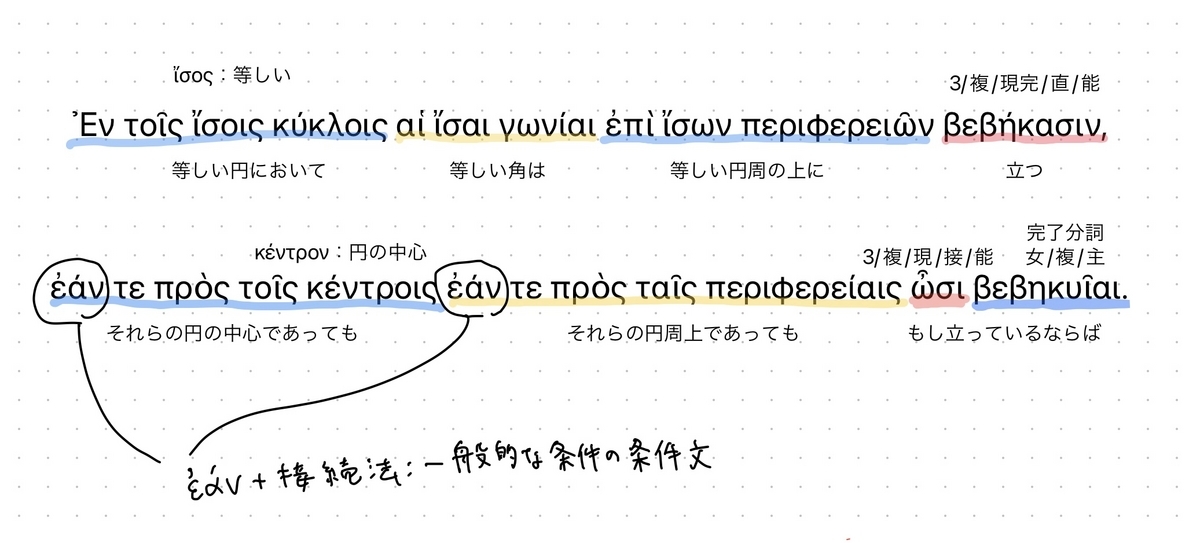
いくつかポイントとなる箇所がある。
まず、二行目に二回登場するἐάνだが、これは英語のifに相当する単語だ。ともに用いる動詞の形によりニュアンスが少しずつ変わるのだが、今回は、ἐάν節(条件節)に接続法現在の動詞が、帰結文に直説法現在完了の動詞がきているので、「一般的な条件の条件文」とわかる。数学の文章にはよく出てくる組み合わせだろう。
注意したいのは、本来なら「一般的な条件の条件文」では、帰結文に現在完了ではなく現在を用いることだ。ただ、今回の場合、使っている動詞が特殊なので、現在完了になっていると考えられる。
というのも、βεβήκασινの原形となる単語はβαίνωなのだが、これは「歩く」「行く」などを意味する単語なのだ。しかし、これを現在完了にすると、「立つ」の意味になる。そういう特殊な単語なので、ここでは現在ではなく現在完了になっていると思われる。
それから、この文章の主語はαἱ ἴσαι γωνίαιで、「等しい角(複数形)」の意味だが、どこの角であるかの説明が抜けている。それが、文の後半の条件節で説明されているわけだ。
この記事の冒頭では、「中心角も円周角も、等しい弧の上に立つ」と訳しているが(つまり参考文献[1]ではそう訳しているが)、元の文に忠実に訳すならこうなるだろうか。
「等しい円において、等しい角は、等しい弧の上に立つ。それが立っているのが中心においてであっても、円周上においてであっても」
ちなみに、今回の記事の証明の中で、「Αにおける角」といった書き方を何度かしているが、これも元のギリシャ語では πρός τῷ Α「Αにおける」と書かれている。
今回の記事は、数学的な話よりギリシャ語の話の方が長くなってしまった。実は最近、古典ギリシャ語を少し勉強したので、今後はこういう記事も増えていくだろう。ただでさえニッチなブログなのに、さらにニッチになりそうである。