第3巻命題32 接弦定理
もし円に直線が接し、その接点から円に対し円を切る直線が引かれるならば、それが接線となす角は円の反対側の切片内の角に等しいであろう。
今回の記事で、なんと当ブログ100個目の記事である。ではこれが『原論』の100番目の命題かというと、残念ながら違う。当ブログには命題以外の記事が二本あるので、今回の命題は98個目の命題である。
さて。今回は接弦定理である。現代の高校では、接弦定理は「円の接線と弦のなす角は、その弦の円周角に等しい」と説明される。命題III.32も同じことを言っているのだが、円周角とは言わずに「反対側の切片内の角」と言っている。面白い表現である。これは元のギリシャ語からそうなっている。
まずは命題の意味を説明する。図のように円ΑΒΓΔに接線が引かれ、その接点から弦ΒΔ(円を切る直線)が引かれたとする。
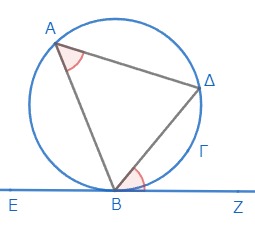
このとき、角ΔΒΖは、それと反対側にある切片内の角ΔΑΒに等しいと述べている。また、もちろん、角ΔΒΕもそれと反対側にある切片内の角ΔΓΒに等しい(図には描いていないが)。
では証明していこう。いま述べた二組の角について、それぞれ証明する。
円ΑΒΓΔに直線ΕΖが点Βで接しているとする。そして、点Βから円を切る直線ΒΔが引かれたとする。
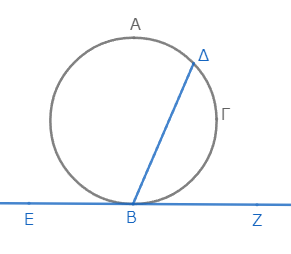
点Βから直線ΕΖに直角に直線ΒΑを引き*1、弧ΒΔ上に任意の点Γを取り、ΑΔ、ΔΓ、ΓΒを結ぼう*2。
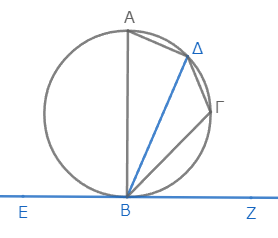
こうすると、直線ΑΒは接線ΕΖに垂直なので、この円の中心は直線ΒΑ上にある*3。つまり、直線ΒΑはこの円の直径である。
さてここで、三角形ΑΒΔに注目する。直線ΒΑが円の直径なので、角ΑΔΒは直角である*4。したがって、三角形ΑΒΔの残りの二角ΔΑΒ、ΑΒΔの和は直角である*5。
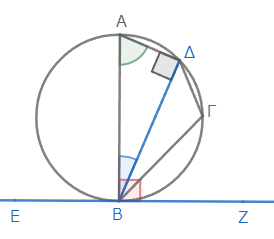
ところで、角ΑΒΖも直角なので、角ΑΒΖは、二角ΔΑΒ、ΑΒΔの和に等しい*6。双方から角ΑΒΔを除こう。すると残りの角ΔΒΖは、円の反対側の切片内の角ΔΑΒに等しい*7。
これで片方が示せたので、もう一方の角についても示そう。
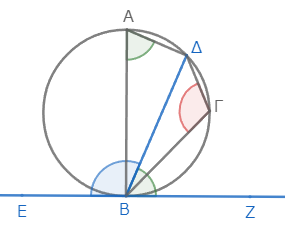
四角形ΑΒΓΔに注目すると、これは円に内接する四角形であるから、その対角の和は二直角に等しい*8。ところで、二角ΕΒΔ、ΔΒΖの和も二直角に等しい*9。ゆえに、二角ΕΒΔ、ΔΒΖの和は、二角ΔΑΒ、ΔΓΒの和に等しく*10、しかもこのうち角ΔΒΖは角ΔΑΒに等しいことは既に示した。したがって、残りの角ΕΒΔは角ΔΓΒに等しい。
よって、もし円に直線が接し、その接点から円に対して円を切る直線が引かれるならば、それが接線となす角は円の反対側の切片内の角に等しいであろう。これが証明すべきことであった。
それほど難しい証明ではない。調べたところ、現代の高校でも本質的にはこれと同じ方法で証明しているようだ。恥ずかしながら、私は全く覚えていなかった。
この証明のままだと、ΒΑが直径のときしか示せていないように感じる。もちろん、命題III.21「円周角の定理」より、同じ切片内の角はすべて等しいので、ΒΑが直径でないときでも接弦定理が成立することがわかる。現代の高校の教科書では、ご丁寧にここまできちんと述べているようだ。
記事の冒頭で、「円周角と言わず、『反対側の切片内の角』と言っている」と書いた。その理由は、元のギリシャ語がそうなっているからだ。ではなぜギリシャ語でそうなっているかといえば、命題の内容を正確に伝えるにはこう書かざるを得なかったからだろう。

この図において、角ΔΒΖに等しいのは角ΔΑΒである。しかし、単に「弦ΒΔに対する円周角」とすると、角ΔΓΒでも良いことになってしまう。角を一意に定めるためには、「反対側」とつけねばならず、反対側を表現するのには切片を持ち出す方が便利だったのだろう。
今回の証明に命題I.13が使われているが、これは第1巻以降、初めての登場だ。久々の活躍である。
命題I.13は、現代風に言えば「直線は180度」という命題であった。『原論』ではもっと周りくどい言い方をしており、「直線が直線の上に立てられて二つの角を作るならば、それらの和は二直角」と述べている。
今回のギリシャ語原文は以下の通り。
̓Εὰν κύκλου ἐφάπτηταί τις εὐθεῖα, ἀπὸ δὲ τῆς ἁφῆς εἰς τὸν κύκλον διαχθῇ τις εὐθεῖα τέμνουσα τὸν κύκλον, ἃς ποιεῖ γωνίας πρὸς τῇ ἐφαπτομένῃ, ἴσαι ἔσονται ταῖς ἐν τοῖς ἐναλλὰξ τοῦ κύκλου τμήμασι γωνίαις.
意味のまとまりごとに訳すと、こうなるだろうか。

分詞や関係代名詞が使われている上、全体が複数の条件がある条件文(英語の仮定法に相当)となっており、非常に複雑な文章となっている。
一行ずつ見ていこう。

一行目は難しくない。文頭のἐάνは英語のifに相当し、文章が条件文(仮定法)であることを示している。「接するなら」と訳したἐφάπτηταίは、ἐφάπτω「結びつける」の三単現の中動態or受動態の接続法である。意味的におそらく中動態である。
中動態とは、能動態と受動態の間みたいなもので、「自分自身に何かをする」や「互いに相手へ何かをする」状況を表す。この文章の場合、直線が自身を円に結びつけている。
接続法とは、話者の主観的な意思などを表すが、ἐάνと合わさることで条件文の条件を表す。
二行目にいこう。

δέは英語のandなどに相当する単語で、前文のἐάνを引き継いでいる。つまり、2つ目の条件を示している。ἀπόは英語のfromに相当し、ἁφῆςはἁφή「接点」の属格である。
難しいのは後半の緑の線を引いた部分だ。ここでは現在分詞τέμνουσαが使われている。これは動詞τέμνω「切る」の分詞である。
古典ギリシャ語の分詞には多種多様な用法があり、私はまだ全然理解できていないので、ほとんど雰囲気で訳している。ただ、これが現在分詞で、主格であることから、次の二点がわかる。
・現在分詞なので、主動詞διαχθῇと同時に起こる
・主格なので、主格の単語τις εὐθεῖαを修飾する
このことから、「ある直線がその円を切りながら引かれた」といった意味になることがわかる。
なお、一行目の文にも直線が出てきたが、こちらの直線εὐθεῖαに定冠詞がついていないことから、一行目の直線と二行目の直線は別物だとわかる。
また動詞διαχθῇも接続法なので、一行目同様、これが条件であることを示している。
ところでδιαχθῇは受動態である。一行目では直線が自分自身を円に接させていたが、こちらは受動的に「引かれて」いる。実は『原論』の文章は、ほとんどの場面で線分が「引かれる」と書かれている(当ブログでは全部「引く」と書いているので、微妙にニュアンスが変わっている)。一行目と二行目で、ユークリッドの主観的に何かが違うっぽいのだが、何が違うのかはよくわからない。あるいは、一行目も受動態で訳すべきなのかもしれない。
三行目にいこう。

文頭のἃςは関係代名詞である。古典ギリシャ語では関係代名詞も格変化し、これは女/複/対である。この場合、女/複の単語を先行詞とし、関係文の中での役割は対格になる。
関係文の中の主語は省略されているが、おそらく二行目の「ある直線」であろう。「ある直線が作る角は(四行目に続く)」という文章になっているはずである。
青線最後のἐφαπτομένῃ「接すること」は現在分詞であり、しかもそれに定冠詞τῇがついている。初めは「なんで分詞に定冠詞が??」と思ったが、おそらくこれは名詞が省略されているのだろう。一行目の「ある直線」が省略され、定冠詞だけが残っているのである。なので、「接線」と訳してよかろう。
黄線を引いたγωνίαςの役割がよくわからない。これがなければ「円を切る直線が接線のもとで作る角は」とすっきり訳せるのだが。
一方で気になるのは、この文章の前に「角γωνία」が登場しないことである。もしかして、関係代名詞の先行詞が関係文の中に入っているのだろうか。
関係代名詞が複数形になっているのは、「円を切る直線と接線が作る角」が二つあるからだろう。命題の証明でもちゃんと二つの角それぞれについて証明していることからも、ユークリッドが二つの角を意識していたことがわかる。
これ以上はよくわからないので四行目にいこう。

二語目のἔσονταは、英語のbe動詞に相当するεἰμίの3人称/複数/未来/中動態/直説法である。中動態なのは、二つの角が互いに等しくなるからだ。そして未来形なのは、これが条件文だからである。
古典ギリシャ語の条件文は、話者の主観などによって、用いる単語や時制が変化する。今回の命題では、
条件節が「ἐάν + 接続法」
帰結節が「直説法未来」
の形になっている。これは、話者が「条件、結果ともに、実現可能性がやや高い」と考えている場合に用いられる形である。
そりゃそうであろう。数学の命題なので、条件が満たされさえすれば結果は生じるだろう。
ただし、条件が満たされるとは限らない。今回の場合、「直線が円に接する」「接点から円を切る直線が引かれる」という二つの条件を満たす必要があり、これらが必ずしも満たされるとは限らないニュアンスが「やや」に現れているのかもしれない。あるいはもしかしたら、「引かれる」と受動態で表していることから、行為者=読者の行動は制限できないという理由
*1:命題1-11「与えられた直線にその上の与えられた点から直角に直線を引くこと」
*3:命題3-19「もし直線が円に接し、接点から接線に直角に直線が引かれるならば、円の中心は引かれた直線上にあるであろう」
*4:命題3-31「円において半円内の角は直角であり、半円より大きい切片内の角は直角より小さく、より小さい切片内の角は直角より大きい。また半円より大きい切片の角は直角より大きく、より小さい切片の角は直角より小さい」
*5:命題1-32「すべての三角形において、一辺が延長されるとき、外角は二つの内対角の和に等しく、三角形の三つの内角の和は二直角に等しい」
*7:公理3「等しいものから等しいものが引かれれば、残りは等しい」
*8:命題3-22「円に内接する四辺形の対角の和は二直角に等しい」
*9:命題1-13「もし直線が直線の上に立てられて二つの角を作るならば、二つの直角か、またはその和が二直角に等しい角を作るであろう」