すべての三角形において、どの二角をとってもその和は二直角より小さい。
「三角形の三つの内角の和は二直角である」ということを我々は知っている。今回の命題は、それよりも弱い定理だ。
前回同様、今回もまた、中途半端な命題である。『原論』にはもちろん三角形の内角の和が二直角であることは登場するのだが、それはやはり命題32にならないと出てこない。
三角形ΑΒΓがあり、辺ΒΓを点Δまで伸ばそう*1。
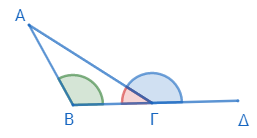
このとき、角ΑΒΓと角ΑΓΒの和が二直角より小さいことを示す。
角ΑΓΔは外角なので、内対角ΑΒΓより大きい*2。
そこで双方に角ΑΓΒを足すと、二角ΑΓΒ、ΑΒΓの和は、二角ΑΓΒ、ΑΓΔの和より小さい*3。ところが二角ΑΓΒ、ΑΓΔの和は二直角に等しい*4。したがって二角ΑΓΒ、ΑΒΓの和は二直角より小さい。
同様にして、二角ΒΑΓ、ΑΓΒの和も、二角ΓΑΒ、ΑΒΓの和も、二直角より小さいことを証明しうる。
よってすべての三角形において、どの二角をとってもその和は二直角より小さい。これが証明すべきことであった。
数式で書けば以下の通り。
角ΑΒΓ<角ΑΓΔ(∵命題16)
ゆえに 角ΑΓΒ+角ΑΒΓ<角ΑΓΒ+角ΑΓΔ=二直角(∵命題13)
今回の命題は、第1巻の後半で上位互換「三角形の内角の和は二直角」が登場する。
上位互換の証明には平行線の性質を使うのだが、その性質の証明には、あの平行線公準が必要になる。
どうやらユークリッドは、平行線公準を使う必要のある命題は、なるべく後ろの方で出したかったらしい。この背景には、「もしかしたら平行線公準は他の公準から証明可能かもしれない」というユークリッドの憂慮があったと考えられている。