公準(要請)次のことが要請されているとせよ。
- 任意の点から任意の点へ直線をひくこと。
- および有限直線を連続して一直線に延長すること。
- および任意の点と距離(半径)をもって円を描くこと。
- およびすべての直角は互いに等しいこと。
- および一直線が二直線に交わり同じ側の内角の和を二直角より小さくするならば、この二直線は限りなく延長されると二直角より小さい角のある側において交わること。
- 同じものに等しいものはまた互いに等しい。
- また等しいものに等しいものが加えられれば、全体は等しい。
- また等しいものから等しいものが引かれれば、残りは等しい。
- また不等なものに等しいものが加えられれば全体は不等である。
- また同じものの二倍は互いに等しい。
- また同じものの半分は互いに等しい。
- また互いに重なり合うものは互いに等しい。
- また全体は部分より大きい。
- また二線分は面積を囲まない。
「要請されているとせよ」とは、妙な言い回しである。
一般的に、これらの公理と公準は、「証明抜きに正しいとすること」とされている。これにはいくつかの意味がある。
「明らかに正しいのに証明できない」という意味や、「間違ってようが正しかろうが、今から考える舞台では正しいものとする」という意味だ。
今から私達は、ユークリッドの編纂した幾何学の舞台で数学をするが、その舞台ではこれら14個の項目はすべて正しいものとする。
もしかしたら間違っているかもしれないが、今から数学をする舞台ではこれらは絶対に正しいものとするという宣言がこの公準と公理である。
この意味では、前回の「定義」も、「証明抜きに正しいとすること」と言えなくもない。
実際、例えば定義3は「線の端は点である」という、定義なんだか定理なんだかわからないことが書かれていた。
定義17にも、「円の直径は円を二等分する」という旨のことが書かれていた。これも定義なのか定理なのかよくわからない。頑張れば証明できそうな気もする。
このブログで参照している『ユークリッド原論』(中村幸四郎ほか/訳、共立出版)の解説を斜め読みしたところ、どうやらユークリッドの時代には、「定義」「公準」「公理」の三つの用語を、あまり区別せずに使っていたらしい。
元々ごちゃごちゃになっていた数学の用語を、定義、公準、公理の三つに分類し整理したのがユークリッドである(という説がある)、みたいな説明が書かれていた。
現代の数学では、一周回ってこの三つをあまり区別していない気がする。ユークリッドの苦労に合掌。
公準1から3は、作図において定木とコンパスで出来ることを規定している。すなわち、定木とコンパスにはそれぞれ次のことしかできない。
定木:任意の二点間を結ぶ or 線分を延長する
コンパス:任意の点を中心に、任意の半径で円を描く
ここで一つ重大なことに気付く。
我々が普段作図するとき、コンパスで「長さを移す」という操作をすることがある。線分の長さにコンパスを開き、そのままコンパスを別の場所に移動させて円を描く、という行為だ。
ところが、『原論』ではそれは禁じ手だ。公準の中に、「任意の長さを任意の場所へ移動させること」という項目が存在しないからだ。コンパスは、紙から持ち上げたら必ず閉じなくてはいけない。
そんな条件で作図できるのか……と不安になるが、可能であることが命題1-2で明らかになる。そのときにまた詳しく書こう。
さてさて、興味深いのは公準4「すべての直角は互いに等しい」である。
「直角=90度」と思っていると「当たり前じゃないか」と言いたくなるところだが、『原論』においては直角=90度ではない。前回の直角の定義を思い出そう。
直線の上に直線が立てられ、接角が互いに等しいとき、その角のことを直角と呼ぶのだった。

この定義だと、あらゆる直線の上で作られる直角がすべて等しいのかどうか、明らかではない。こっちの直線の上とあっちの直線の上では、違う大きさの直角ができるかもしれないのだ。
だが、直線はすべて同じ形なのだから、直角だって等しくなるはずである。少なくとも、直感的には。
そんなわけで、「すべての直角は互いに等しいことは、証明抜きに正しいとしよう」と決めたようだ。
個人的には、公準4が一番影が薄くて可哀想な感じがする。公準が五人姉妹だとすると、1から3は作図のルールを決め、様々な命題に登場するアクティブで社交的な仲良し三人組の少女達だ。公準5は、あとで触れるが、問題ばっかり起こす不良娘である。しかしその実、その問題が新しい数学の一分野を創ってしまったくらいの天才系不良少女だ。
公準4は優秀なんだけど慎まし過ぎて、全く目立たない淑やかな少女である。思わず守ってあげたくならないだろうか。
私はいったい何を言っているのだろうか。
さて、『原論』を語る以上、公準5に触れないわけにはいかないだろう。誰が名付けたか知らないが、「平行線公準」と呼ばれるものだ。再掲しよう。
公準5(平行線公準)
一直線が二直線に交わり同じ側の内角の和を二直角より小さくするならば、この二直線は限りなく延長されると二直角より小さい角のある側において交わること。
長い! わかりにくい!
ほかの公準がすべて一言で終わっているのに、こっちは接続詞「ならば」まで使われてしまっている。これはもう定理なんじゃないのか。
と、ユークリッド自身も思ったようで、公準5が使われる命題は第1巻の後半にならないと出てこない。
おそらくユークリッドも、残り四つの公準から平行線公準を証明しようとしただろう。ユークリッド以降も、多くの数学者がその証明に挑戦した。古いところでは、B.C.100年頃の哲学者ポセイドニオスもこの証明に挑戦したと言われている。
(ちなみに、ユークリッドはB.C.300年頃の数学者である)
ユークリッドの時代から2000年ほど経って、ついに平行線公準は、たしかに公準であることが確かめられた。
つまり、他の四つの公準から証明できない事柄であることがはっきりしたのだ。
それどころか、平行線公準の否定を公準とすると、新しい数学の舞台ができることがわかった。不良少女が天才系不良少女となった瞬間である。
この辺の詳しい話は『原論』の範囲を逸するし、そもそもあまり詳しく知らないので、ここではこれ以上触れない。
ちょっと面白いなと思うのは、平行線公準を否定した舞台では、公理9「二線分は面積を囲まない」も間違いとなる場合がある点だ。
よくよく考えてみると、この二つは数学的に似たようなことを言っている気がする。ユークリッド自身はそのことに気付いていたのだろうか?
平行線公準は文章が長いので面食らってしまうが、言っている内容はとてもシンプルである。図にしてみれば明らかだ。
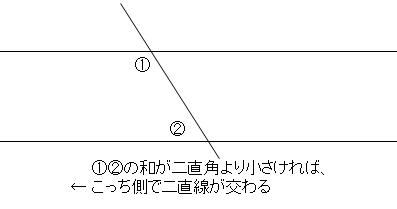
これだけである。二直線は交わるときと交わらないときがあるが、どのようなときにどこで交わるのかについてこの公準は言及している。
これを直感的に正しいと思うかどうかは人によって意見が分かれる気もする。しかし過去に多くの数学者が「直感的に正しいと思えない」と感じ、証明を試みてきたことは既に述べた。
ところでこの図において、公準5は「二直線は左側で交わる」と言っているが、「右側で交わらない」とは言っていない。もしかしたら交わるかもしれない。
しかし、右側でも交わるとすると、公理9「二線分は面積を囲まない」に矛盾する。よって、この図において右側で直線が交わることはない。これが証明すべきことであった。
先ほど言ったように、公準5と公理9は、何かちょっとつながりがある気がする。屋上で授業をサボる不良少女と、彼女の天才性にいち早く気付き一目置いているものの彼女の素行に腹を立てている優等生少女のような関係みたいだ。
私はいったい何を言っているのだろうか。
ちなみに①②の和が二直角のときどうなるかについては、第1巻の後半できちんと証明される。それまで待とう。