第１巻命題35　平行四辺形の等積変形［同底編］

同じ底辺の上にあり、かつ同じ平行線の間にある平行四辺形は互いに等しい。

この命題における「等しい」とは、「面積が等しい」という意味だ。底辺が共通で、同じ平行線の間にある（つまり高さが等しい）平行四辺形は、面積が等しいと言っている。

f:id:kigurox:20180119215235p:plain

二つの平行四辺形ΑΒΓΔとΕΒΓΖが、同じ底辺ΒΓの上にあり、かつ、同じ平行線ΒΓ、ΑΖの間にあるとする。このとき、両者は等しいことを証明しよう。

まず、ΑΒΓΔは平行四辺形なので、辺ΑΔは対辺ΒΓに等しい*1。同様に、ΕΒΓΖも平行四辺形なので、辺ΕΖは辺ΒΓに等しい*2。ともにΒΓに等しいので、ΑΔもΕΖに等しい*3。双方にΔΕを加えれば、ΑΕ全体はΔΖ全体に等しい*4。

f:id:kigurox:20180119214213p:plain

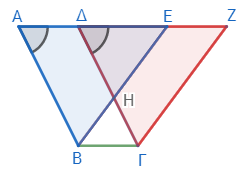
ここで、二つの三角形ΑΒΕとΔΓΖに注目する。すると辺ΑΕは辺ΔΖに等しく、辺ΑΒと辺ΔΓも、平行四辺形の対辺なので互いに等しい*5。さらに二線分ΑΒ、ΔΓは平行線なので、外角ΖΔΓは内対角ΕΑΒに等しい*6。よって二つの三角形ΑΒΕとΔΓΖは、二辺とその間の角がそれぞれ等しいので、（面積が）等しい*7。

f:id:kigurox:20180119214408p:plain

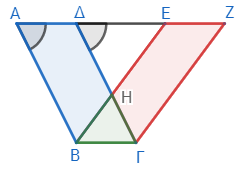
双方から、重なった部分ΔΗΕを引き去ろう。すると残りの不等辺四角形ΑΒΗΔは残りの不等辺四角形ΕΗΓΖに等しい*8。二つの不等辺四角形に、三角形ΗΒΓを加える。すると平行四辺形ΑΒΓΔ全体は、平行四辺形ΕΒΓΖ全体に等しい*9。

よって、同じ底辺の上にあり、かつ同じ平行線の間にある平行四辺形は互いに等しい。これが証明すべきことであった。

今回の証明には、不足している点がある。下図のように、辺ΓΔと辺ΒΕが交わらない場合は、上記の方法では証明できない。

f:id:kigurox:20180119220150p:plain

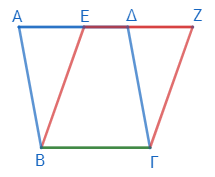
この場合は、二つの三角形ΑΒΕとΔΓΖが互いに等しくなるので、双方に不等辺四角形ΕΒΓΔを加えることで、二つの平行四辺形が等しいことを示せる。

ΑΒΕとΔΓΖが等しいことは簡単に示せる。まずΑΔがΒΓに等しく、ΕΖもΒΓに等しいので、ΑΔとΕΖも互いに等しい。双方からΕΔを引けば、ΑΕはΔΖに等しい。そしてΑΒとΔΓは平行四辺形の対辺なので互いに等しい。さらに角ΕΑΒと角ΖΔΓは平行線ΑΒ、ΔΓの外角と内対角なので、互いに等しい。よって二辺とその間の角がそれぞれ等しいので、三角形ΑΒΕと三角形ΔΓΖは互いに等しい。

ユークリッドは、このことに気付かなかったのだろうか？　それとも、気付いていて敢えて書かなかったのだろうか？

似たような疑問を、命題２４の記事でも書いた。

stoixeia.hatenablog.com

ユークリッドは時々このように、図形を少し変形させた場合の証明を欠いている。もしかしたら本当に気付かなかったのかもしれないが、「ひとつのパターンで証明すれば十分だろう」と考えていたのかもしれない。

現代なら、あらゆるパターンを示して初めて証明終了となる。しかしユークリッドの時代は、数学における証明という概念が登場してから、まだ200～300年しか経っていない。現代とは考え方が大きく違ったのかもしれない。

あるいは、『原論』は初学者のための教科書であったから、あらゆるパターンを網羅するよりは、簡潔さを優先しようとしたのかもしれない。

今回の証明中に「不等辺四角形」という言葉が出てきたが、この言葉が指していた図形はいずれも台形だ。『原論』には「台形」も登場しないのだ。

ちなみに、第１巻の定義２２には、次のようにある。

定義２２

四辺形のうち、正方形とは等辺でかつ角が直角のもの、矩形とは角が直角で等辺でないもの、菱形とは等辺で角が直角でないもの、長斜方形とは対辺と対角が等しいが等辺でなく角が直角でないものである。これら以外の四辺形はトラペジオンと呼ばれるとせよ。

この定義からすると、今回出てきた不等辺四角形は、すべてトラペジオンと呼ばれるべきだ。『原論』ではこのように、定義していない単語が突然出てきたり、定義した単語が一切出てこなかったりする。これは、ユークリッドが複数の書籍を参照しながら『原論』を執筆したためだと言われている。

今回の命題は、
「平行四辺形の面積＝底辺×高さ」
という公式を知っていれば、当たり前のことである。

しかしそれは、話の順序が逆転している。平行四辺形の面積が底辺×高さで求まるためには、底辺と高さが決まれば面積が一定になることが保証される必要がある。今回の命題は、まさにそれを保証するものだ。
（正確にいえば、保証するのは次回の命題だ。今回の命題は底辺が共通である必要があったが、次回は共通でなくとも等しければ十分なことを示す）

話は逸れるが、実は『原論』には「面積を求める公式」が登場しない。我々にとってお馴染みの「底辺×高さ÷２」などが出てこないのだ。

ユークリッドはこれらを知らなかったわけではないだろう。彼は古代バビロニアの数学に通じていたと考えられているが、そこには色々な三角形や四角形の面積を求める公式が存在したと言われている。ユークリッドは、知っていて敢えて書かなかったのだ。

その理由について、カッツ『数学の歴史』100頁には、次のようにある。第７巻「数論」の解説の一部だ。

ユークリッドが第VII巻を一から始めることにしたのは、アリストテレスによる幾何学的な大きさと数との明確な区別に彼が忠実であろうとしたことの証拠である。最初の６巻は幾何学的な大きさ、とくに長さと面積を扱うものであった。第V巻は比例する大きさに関する一般理論を扱っていた。しかし第VII巻から第IX巻においてユークリッドは数のみを扱うのである。それゆえ、第VII巻には第V巻の特殊な場合にすぎないように見える多くの結果が存在するのだが、ユークリッドにとってそれらはまったく別のものなのである。

なんと、アリストテレスは「数と大きさは違う」と考えていたらしい。ユークリッドはそれに倣っているのだ。ユークリッドが数と大きさを結びつけるのは第10巻「無理数論」からである。無理数を扱うために、どうしても面積を使う必要があったようだ。

数と大きさが違うなら、数とはなんだろうか。同書67頁にはこうある。

アリストテレスは数と大きさを「量」という同じ一つのカテゴリーに分類したが、このカテゴリーを離散的なもの（数）と連続的なもの（大きさ）の二つのクラスに分けた。後者の例として、アリストテレスは線や面、立体、時間をあげている。これら二つのクラスの主要な区別は、大きさが「常に可分割的なものどもへと可分割的であるということ」である一方、数の基礎は不可分割的な単位であるという点にある。

つまり、線分や面積はいくらでも半分にできるが、数は半分にしていくといずれ「それ以上分割できない単位（＝１）」になるので、二つの量は異なる種類のものだと主張していたのだ。種類が異なるので、面積を数で表すわけにはいかなかったのだ。