もし二つの円が内側で互いに接し、それらの中心がとられるならば、それらの中心を結ぶ線分は延長されて円の接点におちるであろう。
命題6で、二つの円が接する場合、同じ中心を持たないことを示した。
今回は、それらの異なる中心を結ぶ線分は、円の接点を通ることを示す。なお今回の命題11は「内側で」接する円について論じるが、次の命題12では「外側で」接する円について論じる。
さて、二円ΑΒΓ、ΑΔΕが内側で接し、その接点をΑとする。そして、円ΑΒΓの中心Ζと、円ΑΔΕの中心Ηがとられたとする*1。
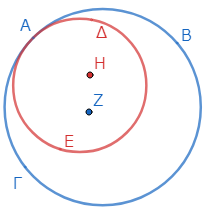
このとき、二点Ζ、Ηを結ぶ線分を延長すると*2*3、点Αに落ちることを示そう(上図では明らかに落ちていないが、これはわざとこのようにしている)。
証明は背理法で行う。
点Θを円ΑΒΓ上の点とすると、これは円ΑΔΕの外部の点である。線分ΖΗΘが引けたとし、ΑΖ、ΑΗを結ぶ*4。
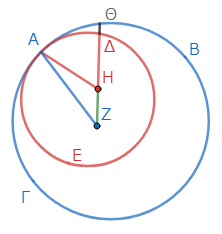
すると、二線分ΑΗ、ΗΖの和は、線分ΖΑより大きい*5。そして、線分ΖΑは線分ΖΘに等しい。ともに円ΑΒΓの半径だからである*6。従って、二線分ΑΗ、ΗΖの和は、線分ΖΘより大きい。
双方から線分ΗΖを引き去ろう。すると、残りの線分ΑΗは、残りの線分ΗΘより大きい。ところが、線分ΑΗは線分ΗΔに等しい。ともに円ΑΔΕの半径だからである*7。したがって、線分ΗΔも線分ΗΘより大きい。しかし、点Θは円ΑΔΕの外部の点なので、線分ΗΔは線分ΗΘよりも小さい*8。すなわち、小さいものが大きいものよりも大きくなる。これは不可能である。
したがって、二点Ζ、Ηを結ぶ線分は、円ΑΔΕの外部に落ちない。ゆえに、点Αにおいて二円の接点に落ちる。
よって、もし二つの円が内側で互いに接し、それらの中心がとられるならば、それらの中心を結ぶ線分は延長されて円の接点におちるであろう。これが証明すべきことであった。
この証明の肝は、第1巻命題20で証明した「三角形の二辺の和は、他の一辺より大きい」である。
円に関する証明であるが、三角形の性質を利用している。円なのに三角形が出てくるのが面白い。
「三角形の二辺の和は、他の一辺より大きい」は、サインコサインと並んで、数学批判のときに槍玉にあがりやすい代物である。いわく、「そんなことは犬でもわかる」とのことだ(この命題は、「遠回りするよりまっすぐ進んだ方が近い」という意味である)。
しかしこの命題を使えば、「内接する二円の中心を結ぶと、接点に落ちる」という、あまり自明でない事柄が示せる。一見役立たなさそうな定理だが、こんなところで役に立つのだ。
次の命題12でも、ほとんど同じ方法で証明を行う。*9