与えられた円の中心を見出すこと。
「与えられた円の中心を作図すること」ではなく、「見出すこと」だそうだ。円に中心があるのは明らかなので、それを改めて作る必要はない、ということだろうか？（←適当に書いているので信じないで欲しい）。
さて、第３巻の本編がいよいよ始まる。最初は円に関する、おそらく最も基本的な定理、円の中心を求めることである。
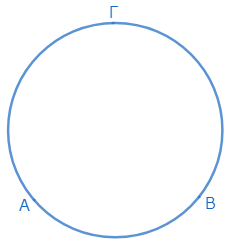
与えられた円をΑΒΓとする。このとき、この円の中心を見出したい。
まず、円を通って任意に線分ΑΒを引き*1、それを点Δで二等分する*2。
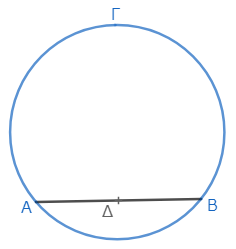（ΑΔ＝ΔΒ）
そしたら、点Δを通りΑΒに直角にΔΓを引き*3、それをΕまで延長する*4。
そして、ΓΕを点Ζにおいて二等分すると、点Ζが円ΑΒΓの中心である。
（ΑΒ⊥ΓΕ、ΕΖ＝ΓΖ）
証明しよう。証明には背理法を使う。
もし点Ζが中心でないとしたら、別の点が中心である。それをΗとして、ΗΑ、ΗΔ、ΗΒが結ばれたとする*5。
ここで、二つの三角形ΑΔΗ、ΒΔΗに注目しよう。すると、辺ΑΔは辺ΔΒに等しく、辺ΗΔは共通である。そして半径であるから、底辺ΗΑは底辺ΗΒに等しい*6。従って二辺が二辺に等しく、底辺が底辺に等しいので、底辺に対する角ΗΔΑはΗΔΒに等しい*7。
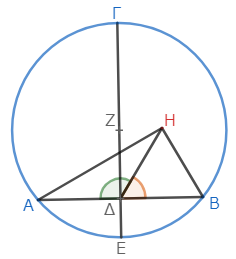
ところが、直線の上に直線が立てられ、接角を等しくするとき、その双方は直角である*8。すなわち、角ΗΔΒは直角である。そして、角ΖΔΒも直角である。従って角ΖΔΒは角ΗΔΒに、すなわち大きいものが小さいものに等しくなる*9*10。だが、これは不可能である。ゆえに、点Ηは円ΑΒΓの中心ではない。同様にして、Ζ以外のいかなる点も中心でないことを証明しうる。
よって、点Ζは円ΑΒΓの中心である。
どういうわけか、この証明には「これが証明すべきことであった」も「これが作図すべきものであった」も書かれていない。理由は知らない。
今回の証明には、一か所抜けがある。気付いただろうか？ 下図のように、点ΗがΓΕ上にある場合は、今回の論法では証明できないのだ。
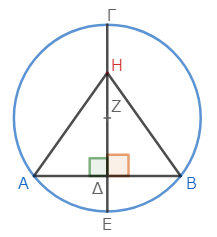
今回の論法では、角ΗΔΒも角ΖΔΒも直角に等しいことから、「大きいものが小さいものに等しい」という矛盾を導いたが、この状態ではこの矛盾は発生しない。
もちろん、この状態でも点Ηが中心でないことは証明できる。
点Ηが中心だと仮定すると、ΗΓとΗΕはともに半径なので等しくなる（すなわち点ΗはΓΕの二等分点になる）。ところがΓΕの二等分点は点Ζなのだった。同じものの半分は互いに等しいので（公理６）、ΖΓとΗΓは互いに等しい。従って大きいものが小さいものに等しい。これは不可能である。よって点Ηは円ΑΓΒの中心ではない。
第１巻の記事でもたびたび述べたが、『原論』ではこのように、あらゆるパターンのうち一つだけを証明して、証明を終えていることがある。この理由について、私は詳しく知らない。
この命題には、系がついている。
第３巻命題１系
これから次のことが明らかである。すなわち、もし円において直線が直線を直角に二等分するならば、円の中心は二等分線上にある。これが証明すべきことであった。
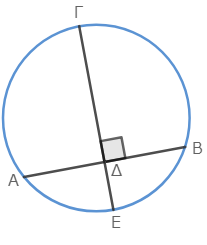
円ΑΒΓにおいて、直線ΓΕが直線ΑΒを点Δで直角に二等分するならば、円の中心はΓΕ上にある、と主張している。今回の命題から明らかなことであるし、現代の我々もよく知っている内容だ。
ただしこの系は、あとの命題であまり活用されていない。このことから、後世の追記とも考えられているようだ。当ブログでは、一応タグ付けしておくが、使うかどうかはわからない。
（2018/06/30追記）
現代の中学では、円の中心は、今回作図した弦の垂直二等分線を二本描き、その交点として見出すようだ。
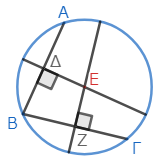
どちらが簡単かと聞かれると微妙なところであるが、こちらの証明には背理法を利用しない。中学生にとっては、こっちの証明の方が簡単なのかもしれない。
ちなみにその証明には、「線分の垂直二等分線は、線分の両端からの距離が常に等しい」という性質を利用する。つまり、ΕΑ、ΕΒが常に互いに等しく、ΕΒ、ΕΓも常に互いに等しいので、ΕΑ、ΕΓも互いに等しい。Α、Β、Γをどのようにとってもこれは明らかに成立するので、Εは円ΑΒΓの中心である、という論法だ。
この作図方法は、のちのち三角形の外心（外接円の中心）を求める際にも利用される。あとへの発展を考えても、こちらの作図の方が都合がよいのだろう。
*2:命題1-10「与えられた線分を二等分すること」
*3:命題1-11「与えられた直線にその上の与えられた点から直角に直線を引くこと」
*6:定義1-15「円とは一つの線に囲まれた平面図形で、その図形の内部にある一点からそれへ引かれたすべての線分が互いに等しいものである」
*7:命題1-8「もし二つの三角形において二辺が二辺にそれぞれ等しく、底辺も底辺に等しければ、等しい辺に挟まれた角もまた等しいであろう」
*8:定義1-10「直線が直線の上に立てられて接角を互いに等しくするとき、等しい角の双方は直角であり、 上に立つ直線はその下の直線に対して垂線と呼ばれる」
*10:公理８「全体は部分より大きい」
