第3巻命題8 円の外部から円周へ引かれた線分
もし円の外部に一点がとられ、その点から円周にいくつかの線分が引かれ、そのうち一つは中心を通り他は任意であるとすれば、凹形の弧に引かれた線分のうち中心を通るものは最も大きく、他の線分のうち中心を通るものに近いものは遠いものより常に大きい、他方凸形の弧に引かれた線分のうち、その点と直径との間のものが最も小さく、他の線分のうち最も小さいものに近いものは遠いものより常に小さく、そしてその点から円周にただ二つの等しい線分が最も小さい線分の両側に引かれるであろう。
長い。
第二巻も長い命題が多かったが、これは輪をかけて長い。なぜこんなに長いかというと、三つのことを同時に主張しているからだ。
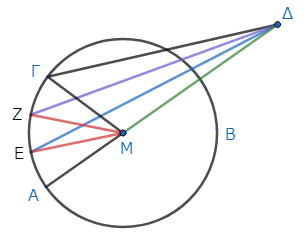
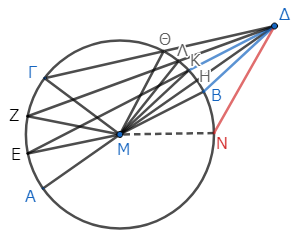
図のように、円ΑΒΓがあり、円外に点Δがあるとする。点Μは円の中心である。
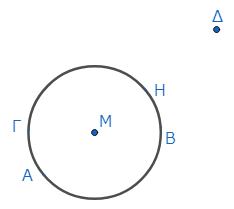
点Δから円周上へ、線分を引こう。線分の引き方として、
・凹形の弧へ引く
・凸形の弧へ引く
の二通りがある。点Δから見て、遠い側の弧が凹形、近い側の弧が凸形である。
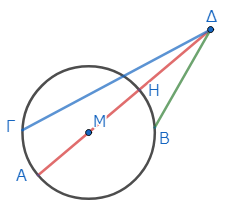
このとき、凹形の弧へ引かれた線分ΔΑ、ΔΓのうち、中心Μを通るΔΑが最も大きく、ΔΑから遠ければ遠い線分ほど小さくなる。これが主張の一つ目である。
そして凸形の弧へ引かれた線分ΔΗ、ΔΒのうち、直径との間にあるΔΗが最も小さく、ΔΗから遠ければ遠い線分ほど大きくなる。これが主張の二つ目である。
最後に、ΔΗの両側に、等しい線分がただ二つだけ引かれる。これが主張の三つ目である。
前回は、円の内部から円周上へ引いた線分について論じた。今回は、円の外部から引いた線分について論じるわけだ。
命題も長いが、証明も長い。根気よく読んでいこう。
まず円ΑΒΓがあり、円の外に点Δがあるとする。そして点Δから、円周上の(凹形の弧の上の)点Α、Γ、Ε、Ζに線分を引く*1。このうち、ΔΑは中心を通る線分としよう。
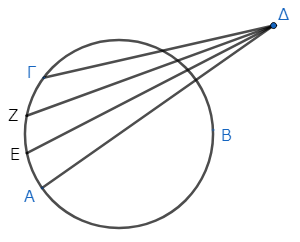
円ΑΒΓの中心をとり*2、それをΜとする。そして、ΜΕ、ΜΖ、ΜΓを結ぶ*3。
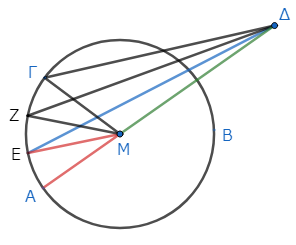
このとき、ΜΑはΜΕに等しい*4。そこで双方にΜΔを加えると、ΔΑはΔΜとΜΕの和に等しい*5。ところで、三角形ΔΜΕに注目すると、ΔΜとΜΕの和は、ΔΕより大きい*6。よって、ΔΑもΔΕより大きい。
さらに、二つの三角形ΔΜΕとΔΜΖに注目しよう。ΜΕはΜΖに等しく、ΜΔは共通であるから、ΜΕとΜΔの和は、ΜΖとΜΔの和に等しい(※)。そして、角ΔΜΕは角ΔΜΖより大きい。二つの三角形において、二辺が二辺にそれぞれ等しく、それらに挟まれる角の一方が他方より大きければ、底辺も大きいので、底辺ΔΕも底辺ΔΖより大きい*7。同様にして、ΔΖがΔΓより大きいことも証明できる。
ゆえに、ΔΑは最も大きく、ΔΕはΔΖより、ΔΖはΔΓより大きい。これが主張の一つ目だった。
次に、凸形の弧の上の点に引いた線分について考える。点Δから凸形の弧の上の点Η、Κ、Λ、Θに線分を引き*8、ΑΗが直径だとする。そして、中心Μから線分ΜΚ、ΜΛ、ΜΘを引く*9。
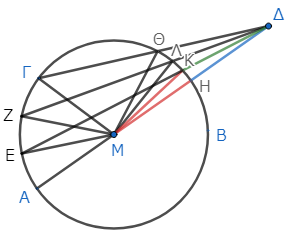
ここで、三角形ΔΚΜに注目しよう。すると、二辺ΜΚ、ΚΔの和は、底辺ΔΜより大きい*10。そしてΜΚはΜΗに等しいので、双方からそれぞれこれらを引くと、残りのΚΔは残りのΔΗより大きい、すなわちΔΗはΚΔより小さい。
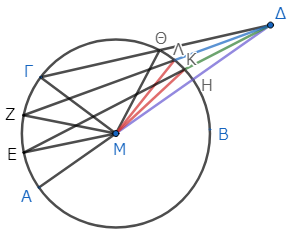
続いて、二つの三角形ΔΜΚ、ΔΜΛに注目しよう。すると、三角形ΔΜΛの内部で、一辺ΔΜを共有する三角形ΔΜΚが作られているから、ΜΚ、ΚΔの和は、ΜΛ、ΛΔの和より小さい*11。そしてΜΚはΜΛに等しいので*12、双方からそれぞれこれらを引くと、残りのΚΔは残りのΛΔより小さい。同様にして、ΛΔはΘΔより小さいことを示せる。
ゆえに、ΔΗは最も小さく、ΚΔはΛΔより、ΛΔはΘΔより小さい。これが主張の二つ目だった。
最後に、点Δから円周上に、等しい線分が二本だけ引けること、しかもそれが最も小さい線分ΔΗの両側に引かれることを示そう。
線分ΔΜ上に、角ΚΜΔに等しい角ΒΜΔを作り*13、ΔΒを結ぶ*14。
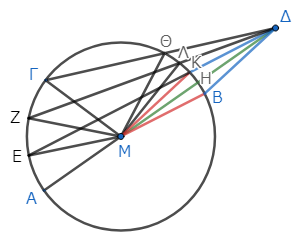
このとき、ΔΚはΔΒに等しくなる。なぜなら、二つの三角形ΚΜΔ、ΒΜΔに注目すると、これらは辺ΜΔが共通で、辺ΜΚが辺ΜΒに等しく*15、等しい二辺に挟まれた角ΚΜΔも角ΒΜΔに等しいので、底辺ΔΚも底辺ΔΒに等しくなるからである*16。
そして、ΔΚに等しい線分は、ΔΒ以外に引かれないことを示そう。
仮に引けたとして、それをΔΝとしよう。するとΔΝはΔΚに等しく、さらにΔΚはΔΒに等しいので、ΔΝもΔΒに等しい*17。しかし、ΔΗに近いものほど小さくなることは、既に示した。従って、ΔΝがΔΒに等しいと、大きいものが小さいものに等しくなってしまうが、これは不可能である。それゆえ、ΔΒ以外のいかなる線分も、ΔΚに等しくなりえない。
よって、もし円の外部に一点がとられ、その点から円周にいくつかの線分が引かれ、そのうち一つは中心を通り他は任意であるとすれば、凹形の弧に引かれた線分のうち中心を通るものは最も大きく、他の線分のうち中心を通るものに近いものは遠いものより常に大きい、他方凸形の弧に引かれた線分のうち、その点と直径との間のものが最も小さく、他の線分のうち最も小さいものに近いものは遠いものより常に小さく、そしてその点から円周にただ二つの等しい線分が最も小さい線分の両側に引かれるであろう。これが証明すべきことであった。
長い。
『原論』にはもっと長い証明がいくらでもあるが、これまでのところでは最長の証明ではなかろうか。おまけに、後半は図がこまごましてしまって、非常に読みづらい(これは私の描き方も悪いのだが)。
証明の途中に、(※)を付けた。前半で、ΔΕとΔΖを比較したときだ。
さらに、二つの三角形ΔΜΕとΔΜΖに注目しよう。ΜΕはΜΖに等しく、ΜΔは共通であるから、ΜΕとΜΔの和は、ΜΖとΜΔの和に等しい(※)。そして、角ΔΜΕは角ΔΜΖより大きい。二つの三角形において、二辺が二辺にそれぞれ等しく、それらに挟まれる角の一方が他方より大きければ、底辺も大きいので、底辺ΔΕも底辺ΔΖより大きい。
ここで、ΜΕとΜΔの和は、ΜΖとΜΔの和に等しいとあるが、 この一文は必要だったのだろうか?
底辺が大きいことを言うためには、二辺が等しく、その間の角が大きいことさえ言えばよい。二辺の和が等しいことは、(結果的にそうなるとしても)言う必要がないのだ。
参考文献[2]には、次のようにある。
後半の部分は、「2辺EM、MDは2辺FM、MDに等しい」の間違いであろうが、英文のEuclid's Elements (Professor D.E.Joyce Clark University)においても、two sides という表現が命題3-7にはあるが命題3-8にはないので、誤訳ではなく、原典そのものにおいてもこのようになっていたものと考えられる。
ここで言っている「後半の部分」が、私の言っている(※)のことである。やはり間違いであると考えるのが妥当のようだ。
これほど長い議論を行う命題8であるが、実は、他の命題にほぼ登場しないようだ。「ほぼ」というのは、命題9で暗に利用されるためである。
しかしその命題9は、命題10の「別証明」でしか利用されない。
当ブログでは扱っていないが、『原論』の命題には別証明が付けられているものが数多くある。しかし参考文献[3]によると、別証明はすべて後世の追記であると考えられているようだ。すると命題9は、後世の誰か*18が命題10の別証明を付す際に書き加えたと考えられる。
となると、命題9にしか利用されない命題8も、後世の追加である可能性が高い。さらに、これと対を成す命題7も、そのとき追加されたと考えるのが自然だろう。
したがって、こんなに苦労して示した命題であるのに、ユークリッド『原論』の原本には登場していない可能性が高いのだ。
だがそのことに落胆する必要はない。参考文献[3]62-63頁には、次のようにある。
したがって『原論』はその原著者とされるエウクレイデスの著作であるその原型が、ヘロン、パッポス、テオンをはじめとする、後世の多くの人々の編集の手を経てできあがった一種の合作と考えるほうが適切であろう。実際、中世以降、現代まで伝承され、数学の歴史に大きな影響を与えた『原論』とは、この、合作としての『原論』であり、もはや回復不可能な「真作」の『原論』ではない。
数学そのものも過去の多くの人々の合作であるが、『原論』もまた、長い歴史が編んだ共著なのである。
*2:命題3-1「与えられた円の中心を見出すこと」
*4:定義1-15「円とは一つの線に囲まれた平面図形で、その図形の内部にある一点からそれへ引かれたすべての線分が互いに等しいものである」
*5:公理2「等しいものに等しいものが加えられれば、全体は等しい」
*6:命題1-20「すべての三角形において、どの二辺をとってもその和は残りの一辺より大きい」
*7:命題1-24「もし二つの三角形において、二辺が二辺にそれぞれ等しく、等しい線分によって挟まれる角の一方が他方より大きいならば、底辺も底辺より大きいであろう」
*10:命題1-20「すべての三角形において、どの二辺をとってもその和は残りの一辺より大きい」
*11:命題1-21「もし三角形の辺の一つの上にその両端から三角形の内部で交わる二線分が作られるならば、作られた二線分はその和が三角形の残りの二辺の和より小さいが、より大きい角を挟むであろう」
*12:定義1-15「円とは一つの線に囲まれた平面図形で、その図形の内部にある一点からそれへ引かれたすべての線分が互いに等しいものである」
*13:命題1-23「与えられた直線上にその上の点において与えられた直線角に等しい直線角を作ること」
*15:定義1-15「円とは一つの線に囲まれた平面図形で、その図形の内部にある一点からそれへ引かれたすべての線分が互いに等しいものである」
*16:命題1-4「もし二つの三角形が二辺が二辺にそれぞれ等しく、その等しい二辺に挟まれる角が等しいならば、底辺は底辺に等しく、三角形は三角形に等しく、残りの二角は残りの二角に、すなわち等しい辺が対する角はそれぞれ等しいであろう」
*17:公理1「同じものに等しいものはまた互いに等しい」
*18:ヘロンと考えらている。