もし二つの円が外側で互いに接するならば、それらの中心を結ぶ線分は接点を通るであろう。
前回の命題11では、二円が内接するとき、その中心を結ぶ線分は円の接点を通ることを示した。
今回は、外接する場合の話である。前回同様、三角形の二辺の和が、他の一辺より大きくなることを利用する。ただし、利用の方法は、前回とは異なる。さほど難しい内容ではないので、さらっと証明して終わりにしよう。
さて、二円ΑΒΓ、ΑΔΕが、外側で点Αにおいて互いに接しているとする。そして、二円の中心Ζ、Ηを取ろう*1。
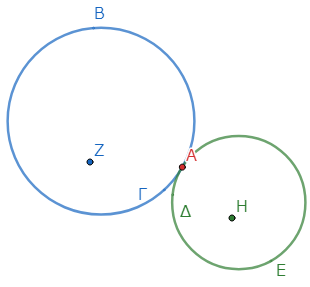
このとき、線分ΖΗは点Αを通ると主張している。
証明には背理法を使う。Ζ、Ηを結んだとき、線分ΖΓΔΗのようになるとしよう。
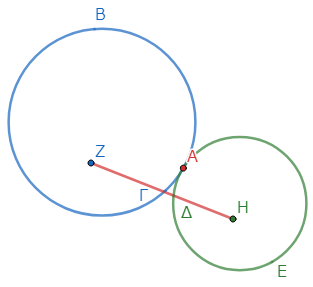
そして、ΑΖ、ΑΗを結ぼう*2。
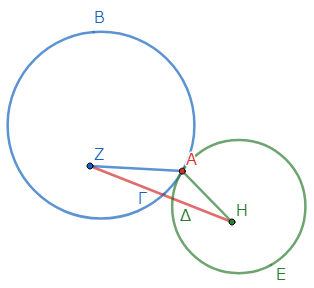
さて、こうすると点Ζは円ΑΒΓの中心なので、線分ΖΑは線分ΖΓに等しい*3。同様に、点Ηは円ΑΔΕの中心なので、線分ΗΑは線分ΗΔに等しい*4。
以上から、二線分ΖΑ、ΗΑの和は、二線分ΖΓ、ΗΔの和に等しい*5。ところで線分ΖΗ全体は、三線分ΖΓ、ΓΔ、ΔΗの和なので、二線分ΖΓ、ΗΔの和より大きい。よって、線分ΖΗ全体は、二線分ΖΑ、ΗΑの和より大きい。
ここで、三角形ΑΖΗに注目しよう(二線分は面積を囲まないので*6、ΖΓΔΗが線分ならΖΑΗは線分ではない。したがってこれは三角形になる)。すると、辺ΖΗは二辺ΖΑ、ΗΑの和より小さい*7。しかし、ΖΗはΖΑ、ΗΑの和より大きいことも、先に証明した。これは矛盾である。従って、二点Ζ、Ηを結ぶ線分は、点Α以外の点を通らない。ゆえに点Αを通る。
よって、もし二つの円が外側で互いに接するならば、それらの中心を結ぶ線分は接点を通るであろう。これが証明すべきことであった。
とても面白い証明である。前回同様、円の話をしているのに、突然三角形が出てくるところがお茶目で良い。
参考文献[1]の文章では、三角形に注目したことを説明せず、いきなり以下のように書かれている。
それゆえΖΑ、ΑΗの和はΖΓ、ΗΔの和に等しい。ゆえにΖΗ全体はΖΑ、ΑΗの和より大きい。ところがまた小さくもある。これは不可能である。
いきなり「ところがまた小さくもある」と出てくるのだ。参考文献[3]の文章でもそうなっているので、『原論』の原文がそうなっていると思われる。私は最初これを読んだとき、なぜ小さくもあるのかわからなかった。参考文献[3]の説明を読んで、ようやく理解した。
ちなみにこの命題は、後世のヘロンによって追加されたものと言われているようだ。『原論』の古い写本にはこの命題はなく、したがって、これ以降の命題番号がひとつずつズレるようである。