同じ線分の上の同じ側に、円の相似で不等な二つの切片は作られ得ない。
命題20~22まで、ひとつの円における円周角や中心角の性質を見てきた。
ここからは、二つの等しい円におけるこれらの性質を見ていく……のだが、今回はそのための準備である。準備はしばらく続く。
さて準備の最初は、円の切片に関するものである。同一の線分上の同じ側には、相似だが不等な二つの切片は作れない、と主張している。言い換えると、同一の線分上の同じ側には、合同な切片か、不等な切片しか作れない、ということになる。
円の切片(τμῆμα κύκλου)とは、次のようなものであった。
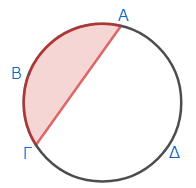
円ΑΒΓΔにおいて、弦ΑΓと弧ΑΒΓに囲まれた部分のことだ。現代の数学ではあまり聞かない用語である。
また、「相似な切片」とは、そのままの意味で、ある切片を拡大縮小した図形を、元の切片の相似な切片と呼ぶ。が、『原論』の第3巻ではまだ比例の概念が使えないため、次のように定義する。
第3巻定義11
二円の相似な切片とは、等しい角を含む、すなわち切片内の角が互いに等しいものである。
要は、円周角の等しい切片のことを、相似な切片と呼ぶ。相似な図形は対応する角が等しくなる性質があるので、これでも定義できるのである。
前置きが長くなった。証明に入ろう。用語は特殊だが、証明は簡単である。
証明は背理法で行う。仮に、線分ΑΒ上の同じ側に、円の相似で不等な二つの切片ΑΓΒ、ΑΔΒが作られたとする。

そしたら、ΑΓΔを結び、ΓΒ、ΔΒを結ぼう*1。

すると、切片ΑΓΒは切片ΑΔΒに相似であるから、角ΑΓΒは角ΑΔΒに等しくなる(それが相似な切片の定義であった)*2。すると、三角形ΓΔΒにおいて、外角が内角に等しくなる。しかし、これは不可能である*3。
よって、同じ線分の上の同じ側に、円の相似で不等な二つの切片は作られ得ない。これが証明すべきことであった。
ごく短い証明である。それほど難しいところもないだろう。
登場する命題も、命題I.16ただひとつである。
この命題I.16は、これまでは三角形の合同条件(二辺両端角相当)や「錯角が等しければ平行」など、割と重要どころにひょっこり登場した命題である。そして今回も、今後の命題群に続く重要な命題の証明にひょっこり登場している。一見地味だが、なかなか縁の下の力持ちな命題である。
ところで今回の証明には、第1巻命題21を使ってもよさそうである。
もし三角形の辺の一つの上にその両端から三角形の内部で交わる二線分が作られるならば、作られた二線分はその和が三角形の残りの二辺の和より小さいが、より大きい角を挟むであろう。
三角形の内部に、底辺を共有する三角形を作ると、その頂角は元の三角形の頂角より大きくなる、という命題である。ちょうど、今回の命題でも、三角形ΑΔΒの内部に三角形ΑΓΒを作っていた。

しかし、命題I.21は、三角形の二つの低角からそれぞれ線分を延ばすことを前提としている。底辺以外の辺を共有することは、想定されていないように見える。なので、今回の状況には適用しにくいのかもしれない。
それにそもそも、命題I.21の証明にも、命題I.16は使われている。だったら、命題I.16を使った方が、証明としてスマートであろう。