円において直径は最も大きく、他の弦のうち中心に近いものは遠いものより常に大きい。
前回の命題14で、中心からの距離が等しい弦は大きさが等しいことを示した。
今回は、中心からの距離が異なる場合について言及している。中心に近ければ近いほど大きく、そして中心を通る弦(直径)が最も大きくなる、というのが命題の主張だ。
さくっと証明しよう。
ΑΒΓΔを円、弦ΑΔをその直径、点Εを中心とする。そして、弦ΒΓは直径に近く、弦ΖΗは遠いとする。
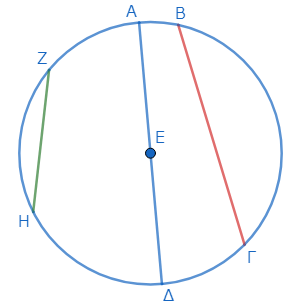
このとき、弦ΑΔは最も大きく、弦ΒΓは弦ΖΗより大きいことを示す。
まずは補助線を引こう。中心Εから、二弦ΒΓ、ΖΗに垂線ΕΘ、ΕΚをそれぞれ引く*1。すると、弦ΒΓは中心に近く、弦ΖΗは遠いから、垂線ΕΘは垂線ΕΚより大きい*2。
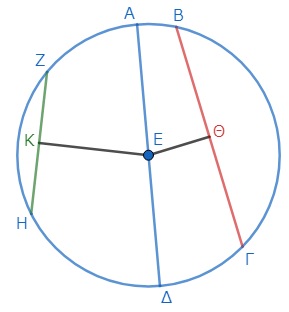
そこで、線分ΕΚから線分ΕΘに等しい線分ΕΛを切り取る*3。点Λを通り線分ΕΚに直角に線分ΛΜを引き*4、それをΝまで延長しよう*5。
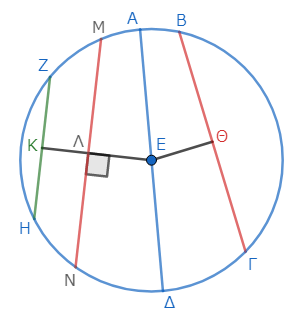
このとき、弦ΒΓは、弦ΜΝに等しい。なぜなら、中心からΒΓに下ろした垂線ΕΘが、ΜΝに下ろした垂線ΕΛに等しいからである*6。
そしたら、二線分ΕΜ、ΕΝを引こう*7。まずはこの状態で、直径ΑΔが他の弦ΒΓより大きいことを示す。
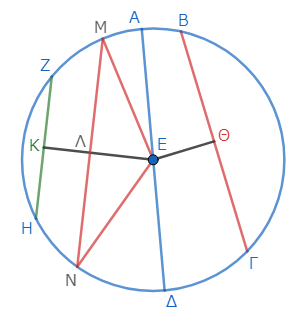
円の半径なので、線分ΕΑは線分ΕΜに、線分ΕΔは線分ΕΝに等しい*8。従って直径ΑΔは、二線分ΜΕ、ΕΝの和に等しい。
ところで、ΕΜΝは三角形なので、二辺ΜΕ、ΕΝの和は辺ΜΝより大きい*9。しかも先述の通り、辺ΜΝは弦ΒΓに等しい。よって、直径ΑΔは線分ΜΝより大きく、ΜΝはΒΓに等しいので、ΑΔはΒΓより大きい(※)。
これで、直径は他のいかなる弦よりも大きいことが示された。
次に、中心に近い弦ΒΓが遠い弦ΖΗより大きいことを示そう。そのために、二線分ΕΖ、ΕΗを引く*10。
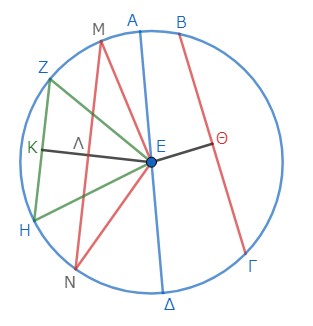
ΕΜΝもΕΖΗも三角形であり、二辺ΕΜ、ΕΝは、二辺ΕΖ、ΕΗにそれぞれ等しい。しかも角ΜΕΝは角ΖΕΗより大きいから、底辺ΜΝも底辺ΖΗより大きい*11。
ところが、線分ΜΝは弦ΒΓに等しいのであった。ゆえに、弦ΒΓも弦ΖΗより大きい。
よって、円において直径は最も大きく、他の弦のうち中心に近いものは遠いものより常に大きい。これが証明すべきことであった。
「弦の大きさ」を、補助線を使って「三角形の底辺」に置き換えるところが、優れた発想である。
証明の途中で(※)を付けた。直径が最大であることを証明した部分である。そこでは、下図を利用してΑΔが最大であることを示した。

証明の流れは、
1.ΒΓはΜΝに等しく、
2.ΜΝは「ΜΕとΕΝの和」より小さく、
3.「ΜΕとΕΝの和」は直径ΑΔに等しいので、
4.ΒΓはΑΔより小さい(ΑΔはΒΓより大きい)
というものであった。
しかしよく考えると、次のような図を描いた方が話が簡単である。
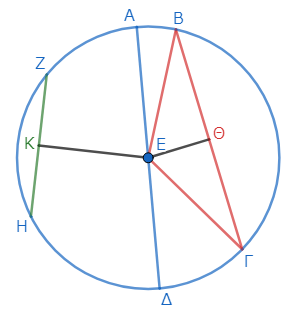
この図において、
1.ΒΓは「ΒΕとΕΓの和」より小さく、
2.「ΒΕとΕΓの和」は直径ΑΔに等しいので、
3.ΒΓはΑΔより小さい
となる。
ユークリッドがこのようにしなかったのは、言うまでもなく、証明の後半でΜΝを使いたかったからだろう。ΖΗがΒΓより小さいことを言うためには、ΜΝとΒΓが互いに等しいことを言わねばならない。それを後半で証明するよりは、前半部分でついでに証明してしまった方がわかりやすいと判断したのだろう。
*1:命題1-12「与えられた無限直線にその上にない与えられた点から垂線を下ろすこと」
*2:定義3-5「大きい垂線が下ろされる弦は、大きい距離にあると言われる」
*3:命題1-3「二つの不等な線分が与えられたとき、大きいものから小さいものに等しい線分を切り取ること」
*4:命題1-11「与えられた直線にその上の与えられた点から直角に直線を引くこと」
*6:命題3-14「円において等しい弦は中心から等距離にあり、中心から等距離にある弦はまた互いに等しい」
*8:定義1-15「円とは一つの線に囲まれた平面図形で、その図形の内部にある一点からそれへ引かれたすべての線分が互いに等しいものである」
*9:命題1-20「すべての三角形において、どの二辺をとってもその和は残りの一辺より大きい」
*11:命題1-24「もし二つの三角形において、二辺が二辺にそれぞれ等しく、等しい線分によって挟まれる角の一方が他方より大きいならば、底辺も底辺より大きいであろう」