もし平行四辺形が三角形と同じ底辺を持ち、かつ同じ平行線の間にあれば、平行四辺形は三角形の二倍である。
三角形の面積は「底辺×高さ÷2」で求められる。ではなぜ2で割るのか、という疑問の答えが、この命題だ。
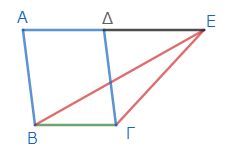
平行四辺形ΑΒΓΔと、三角形ΕΒΓが、同じ底辺ΒΓをもち、かつ同じ平行線ΑΕ、ΒΓの間にあるとする。このとき、ΑΒΓΔ(の面積)がΕΒΓの二倍であることを示そう。
まず補助線として、ΑΓを結ぶ*1。
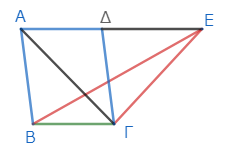
すると、いまできた三角形ΑΒΓは、三角形ΕΒΓに等しい。なぜなら、同じ底辺ΒΓの上にあり、同じ平行線ΒΓ、ΑΕの間にあるからだ*2。
そして、平行四辺形ΑΒΓΔは、三角形ΑΒΓの二倍である。なぜなら、対角線ΑΓが、平行四辺形ΑΒΓΔを二等分しているからだ*3。
ゆえに、平行四辺形ΑΒΓΔは、三角形ΕΒΓの二倍でもある。
よってもし平行四辺形が三角形と同じ底辺を持ち、かつ同じ平行線の間にあれば、平行四辺形は三角形の二倍である。これが証明すべきことであった。
簡単な証明であろう。比較したい三角形に等しい三角形を、平行四辺形の内部に作図し、それが平行四辺形の半分であることを示した。
今回の命題は同じ底辺を持つ平行四辺形と三角形の話だったが、等しい底辺を持つ場合でも、以下の図で同様に証明できる。
 (ΒΓ=ΖΗ、ΒΗ // ΑΕ)
(ΒΓ=ΖΗ、ΒΗ // ΑΕ)
しかし『原論』ではどういうわけか、この場合の証明は行わない。命題35から40まで、ずっと「同じ底辺」「等しい底辺」と交互に扱ってきたのに、ここで唐突に同じ底辺しか論じないのは、どうにも不自然である。
理由は知らないが、もしかしたらピタゴラスの定理の証明に不要だからかもしれない。今回の命題はピタゴラスの定理の証明で大活躍するのだが、等しい底辺を持つ場合は不要なのだ。
この推論は、「ユークリッドはピタゴラスの定理を示すために『原論』第1巻を書いた」という俗説に基づいている。正直、私自身はこの説を支持していないだが、他に適当な理由が思いつかなかった。
何かそれっぽい理由は、他にないだろうか?