等しい底辺の上にあり、かつ同じ側にある等しい三角形は同じ平行線の間にある。
前々回の命題38で、等底で同じ平行線の間にある三角形は、面積が等しいことを示した。今回は、その逆である。
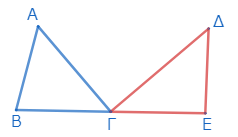（ΒΓ＝ΓΕ）
二つの三角形ΑΒΓ、ΓΔΕが互いに等しく、かつこれらの底辺ΒΓ、ΓΕがそれぞれ等しいとする。このとき、両者は同じ平行線の間にあることを示す。
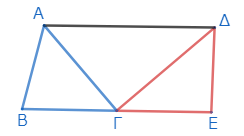
つまり、ΑΔを結んだとき*1、ΑΔがΒΕに平行であることを示す。
証明方法は、前回の命題３９とほとんど同じだ。背理法を使い、ΑΔ以外のいかなる線分も、ΒΕに平行にならないことを示そう。
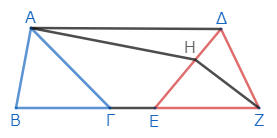
ΑΔが平行でないとし、点Αを通りΒΕに平行な直線を引く*2。それとΓΔとの交点をΖとし、ΖΕを結ぶ*3。
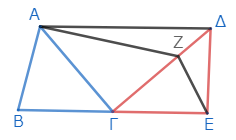（ΒΕ // ΑΖ）
すると、三角形ΑΒΓは三角形ΖΓΕに等しい。なぜなら、底辺が等しく、同じ平行線ΒΕ、ΑΖの間にあるからだ*4。そしてΑΒΓはΔΓΕにも等しかったので、ΖΓΕもまたΔΓΕに等しい*5。しかし全体は部分より大きいので、これは小さいものが大きいものに等しいことになってしまう*6。これは不可能である。よってΑΖはΒΕに平行でない。
同様にして、下図のように、点ΖがΔについてΓと反対側にある場合にも、ΑΖが平行でないことが示せる。
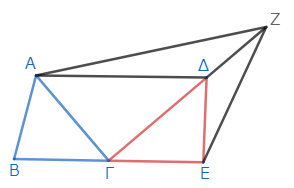
ゆえに、ΑΔ以外のいかなる直線も、ΒΕに平行でない。したがって、ΑΔはΒΕに平行である。
よって等しい底辺の上にあり、かつ同じ側にある等しい三角形は同じ平行線の間にある。これが証明すべきことであった。
前回と全く同じ証明方法であることがわかるかと思う。
文章も、意図的にほとんど同じにしてある。『原論』でも、ほぼ同じ文章が書かれている。
そういえば、前回も今回も証明の最後の部分で、平行線が少なくとも一本引けることを前提としている。上の証明は、ΑΔ以外の線分が平行にならないことを示しているだけで、ΑΔが平行であることを直接示しているわけではない。平行線が一本も引けない場合がある世界だったら、この証明では不十分だ。
しかし、平行線が少なくとも一本引けることは、命題３１が（暗に）保証している。よって、この証明で安心して納得してよい。
今回の図で、二つの三角形が頂点Γを共有していた。これが気になった人がいるかもしれない。私も気になった。どういうわけか、『原論』ではこのような図を描いているのだ。だがもちろん、以下のような図でも、同様に証明できる。
そもそも、今回の命題の“もと”である命題３８では、二つの三角形は離れていた。それを敢えてくっつける理由は、よくわからない。
もしや今後この命題を使う際は、くっついている図を利用するのかなと思ったのだが、第１巻では今後、この命題を使わない。
もしかしたら、第２巻以降で登場するのかもしれない。そのときにどんな形で出てくるか、楽しみに待っていよう。
（2018/05/06追記）
参考文献[3]によると、どうやらこの命題は後世の追加だと考えられているようだ。どうりで、この命題が他の命題で利用されていないわけである。
