与えられた直線上にその上の点において与えられた直線角に等しい直線角を作ること。
命題2で、長さ(線分)を移動させる作図を証明した。
実際に作図するときは、 わざわざこの命題を使わずに、コンパスで長さを移しとってしまう人がほとんどだろう。ユークリッドもそうしたに違いない。
ところで、私は中学時代、「長さはコンパスで移せるけど、角度って移せないよなぁ」と思っていた。
だが、実は可能だ。それが今回の命題である。
与えられた直線ΑΒの上に、与えられた直線角ΔΓΕを移したい。しかも、点Αにおいて、だ。

まず、角を作る二直線ΓΔ、ΓΕの上に、任意の二点Δ、Εを取り、ΔΕを結ぶ*1。
そして三線分ΓΔ、ΔΕ、ΕΓに等しい三線分から、三角形ΑΖΗを作る*2。このとき、ΓΔはΑΖに、ΔΕはΖΗに、ΕΓはΗΑに等しくなるようにする。
 (ΓΔ=ΑΖ、ΔΕ=ΖΗ、ΕΓ=ΗΑ)
(ΓΔ=ΑΖ、ΔΕ=ΖΗ、ΕΓ=ΗΑ)
このとき、角ΖΑΗが求める角である。
証明は簡単だ。二つの三角形は、作図の方法から、二辺ΔΓ、ΕΓがΖΑ、ΗΑにそれぞれ等しい。さらに底辺ΔΕもΖΗに等しい。よって底辺に対する角ΔΓΕは角ΖΑΗに等しい*3。
よって与えられた直線ΑΒ上にその上の点Αにおいて与えられた直線角ΔΓΕに等しい直線角ΖΑΗが作られた。これが作図すべきものであった。
要は、角を移したいときは、その角を含む三角形と合同な三角形を作図すればよいのだ。どうして私は、こんな簡単なことに気付かなかったのだろう。
ところでこの作図、前回の命題22を使っているわけだが、実は命題22をそのまま使おうとすると、ちょっとややこしいことになる。
命題22の作図は、最終的に下図のようになった。
半直線ΔΕ上に三角形を作っているわけだが、ここで注目したいのはΔは三角形の頂点ではないということだ。しかし今回の作図では、半直線ΑΒ上に、Αを頂点に持つ三角形を作図しないといけない。命題22を馬鹿正直に使ってしまうと、下図のようになってしまうのだ。

角ΘΖΗは角ΔΓΕに等しいが、点Ζ上に角を作ってもしょうがない。我々は点Α上に角を作りたいのだ。
命題22で点Δが頂点に含まれない理由は、直線ΔΕから、線分Αに等しい長さΔΖを切り取っているからだ。なので、この操作をやらず、次のように作図すればよい。

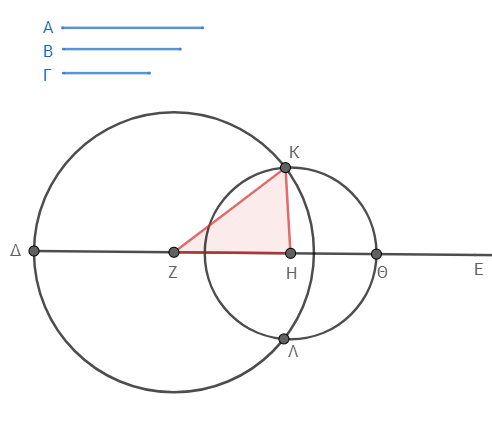
まず直線ΑΒから、線分ΓΔに等しい線分ΑΖと、線分ΓΕに等しい線分ΑΚを切り取る。そして直線ΚΒから、線分ΕΔに等しい線分ΚΝを切り取る。そして中心Α、半径ΑΖの円ΖΗΘと、中心Α、半径ΑΚの円ΚΛΜと、中心Κ、半径ΚΝの円ΝΛΗを描く。そしてΗΑを結べば、角ΗΑΚが角ΔΓΕに等しくなる。
もちろん本質的には命題22と同じ作図である。命題22では、長さを三回切り取っていたが、その最初の一回をやらなかっただけだ。
むしろ、どうして命題22でこのように作図していないのかが疑問である。こちらの方が、描きたい場所にきちっと三角形を描けると思うのだが。
もしかしたら、「このくらいのこと、言わなくてもわかるでしょ」と考えたのかもしれない。確かに、文章で説明するとややこしいが、実際に手を動かしてやってみればすぐにわかることだ。
あるいは、理論上可能かどうかだけ考えていて、実際的に使いやすいかどうかまでは考えていなかったのかもしれない。命題2の線分の移動にしたって、実際に作図するときに毎回できるかと言えば、まず無理である。
「理論上可能であるから、実際には難しくても作図できるものとする」という判断には、だいぶ高度な抽象的思考が必要な気がする。数学は大昔から抽象的な学問だったのかもしれない。
他に考えられる理由は、「切り取る」という表現に見え隠れしている気がする。線分ΑΒから短い線分を切り取ったあと、また点Αから延びる線分を切り取るのはおかしい、と考えたのかもしれない。
ギリシャ語が分かれば「切り取る(απολαμβανειν)」という言葉のニュアンスがわかるのかもしれないが、残念ながら私にはギリシャ語が分からない。そのうち詳しい文献に当たってみよう。