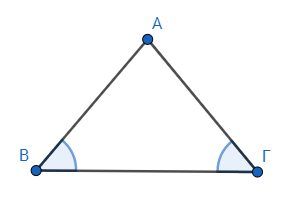
もし三角形の二角が互いに等しければ、等しい角に対する辺も互いに等しいであろう。
前回は二等辺三角形の底角が等しいことを示した。
今回はその逆である。前回ほどややこしくないが、ちょっと戸惑う証明かもしれない。私は理解するのに少し時間がかかった。
三角形ΑΒΓがあり、角ΑΒΓが角ΑΓΒに等しいとする。このとき、辺ΑΓ＝辺ΑΒとなることを示す。
証明には背理法を使う*1。もし辺ΑΒとΑΓが等しくないとすれば、どちらかは大きい（これは公理にはないが、暗黙の了解として使っている）。ΑΒを大きいとして、ΑΒからΑΓに等しい線分ΔΒを切り取り*2、ΔΓを結ぶ*3。
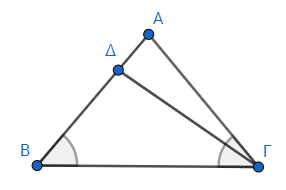（ΑΓ＝ΔΒ）
ここで、二つの三角形ΑΓΒとΔΒΓに注目しよう。
するとこれらは、ΑΓがΔΒに等しく、ΒΓが共通で、さらに角ΑΓΒと角ΔΒΓが等しい。したがって二辺とその間の角が等しいので、底辺ΑΒは底辺ΔΓに等しく、三角形ΑΓΒは三角形ΔΒΓに等しい*4。
すると、小さいものが大きいものに等しくなってしまう（※）。これは不合理である。それゆえΑΒはΑΓに不等ではない。ゆえに等しい。
よってもし三角形の二角が互いに等しければ、等しい角に対する辺も互いに等しいであろう。これが証明すべきことであった。
私がこれの理解に苦労した理由は、（※）印の部分だ。この部分は参考文献の文章*5でも主語が曖昧で、何が小さくて何が大きいのかわからなかったのだ。少なくとも、次の三通りの解釈が可能なはずだ（図は再掲）。
ひとつ。「三角形ΔΒΓは三角形ΑΓΒより小さい」という解釈。
点Δが線分ΑΒ上にあるのだから、三角形ΔΒΓは三角形ΑΓΒの一部だろう。「全体は部分より大きい」という公理８から、「部分（ΔΒΓ）と全体（ΑΒΓ）が等しくなるので不合理」という意味だと解釈できる。
ふたつ。「底辺ΔΓは底辺ΑΒより小さい」という解釈。
直前の文章にこの底辺への言及があるので、始めはこのことを言っているのかと思ってしまった。だが、パッと見でこの二つのどちらが大きいか、わかるだろうか？ 少なくとも私にはわからない。というか、条件が足りなくて大きいとも小さいとも言えないはずである。
そして三つ。「角ΔΓΒは角ΑΒΓより小さい」という解釈。
角ΔΓΒは明らかに角ΑΓΒより小さいが、角ΑΓΒ＝角ΑΒΓなのだから、角ΔΓΒは角ΑΒΓより小さくないといけない。しかしこの二つが等しいことになってしまうので不合理である、という解釈だ。だが直前までこの角への言及が無いのに、突然これを持ち出すのは不自然であろう。
というわけで、たぶん一つ目の解釈が妥当なのだが、私はこの解釈に至るまでに時間を要したのだった。皆さんは瞬時にご理解頂けただろうか。
ところで、「ある三角形が別の三角形より小さい」という表現は、数学的にアリなのだろうか？ 相似形ならこういう言い方もするだろうし、面積を比較して言うこともあるだろう。
しかしここで言及している三角形は相似ではないし、面積を比較しているわけでもない。日常的な用語として、見た目のサイズが違う三角形を「大きい／小さい」と呼ぶことはあるから、ここでの「小さい」は日常的な意味の言葉なのかもしれない。
